1 Inform you about time table of exam 2 Inform you about new question papers 3 New video tutorials informationIf 2 x 2 y = 2 xy, then dy/dx is equal to If 2 x 2 y = 2 xy , then dy/dx is equal to (1) (2x 2y)/ (2x– 2y)Transcribed image text Use implicit differentiation to find dy/dx and d y/dx y2x2 7 y2x2 x d'y y dx dy O A dx d2y y2x x а2у dy Ов dx У' dx2 y3 x dy yx dy Ос dx y' dx у?

Find Dx Dy For X2 Xy Y2 100 Mathematics Shaalaa Com
2^x 2^y=2^x y find dy/dx at x=y=1
2^x 2^y=2^x y find dy/dx at x=y=1- dy/dx=x/y x^2y^2=1 Differentiate wrt x d/dxx^2d/dxy^2=d/dx1 We already know how to deal with the first and third terms, so lets get them out the way d/dxx^2d/dxy^2=d/dx1 2xd/dxy^2=0 For the remaining term we use the chain rule, we don't know how to differentiate y^2 wrt x but we do know how to differentiate y^2 wrt y (it the same as differentiating x^2 wrt x!)Since 2 2 is constant with respect to x x, the derivative of 2 2 with respect to x x is 0 0 2 x 0 2 x 0 Add 2 x 2 x and 0 0 2 x 2 x 2x 2 x Reform the equation by setting the left side equal to the right side y' = 2x y ′ = 2 x Replace y' y ′ with dy dx d y d x dy dx = 2x d y d x = 2 x




Implicit Differentiation
Calculus Find dy/dx x^2y^2=2xy x2 y2 = 2xy x 2 y 2 = 2 x y Differentiate both sides of the equation d dx (x2 y2) = d dx (2xy) d d x ( x 2 y 2) = d d x ( 2 x y) Differentiate the left side of the equation Tap for more steps Differentiate Tap for more steps Explanation differentiate implicitly with respect to x noting that d dx (y) = dy dx and d dx(y2) = 2y dy dx differentiate xy using the product rule 2xdy dx 2y 2ydy dx = 1 dy dx dy dx(2x 2y− 1) = 1 −2y dy dx = 1 −2y 2x 2y− 1 Answer linkCalculus Find dy/dx y^2=1/ (1x^2) y2 = 1 1 − x2 y 2 = 1 1 x 2 Differentiate both sides of the equation d dx (y2) = d dx ( 1 1−x2) d d x ( y 2) = d d x ( 1 1 x 2) Differentiate the left side of the equation Tap for more steps
Question Find Dy/dx By Implicit Differentiation X^2/x Y = Y^2 6 Y' = (y^2 6) (2x 2y 2)/(x) (2xy 3y^2 6) This problem has been solved!It is given that matht(1x^2)=x \qquad/math and math\qquad x^2t^2=y/math matht(1x^2)=x \qquad \Rightarrow \qquad t=\frac{x}{1x^2}/math mathx^2t^2 How do you use implicit differentiation to find dy/dx given #x^2y^2=2#?
*Thanks for the A* First off, notice that this differential equation is of the form M(x,y)dxN(x,y)dy=0, and notice that this differential equation, in current form, is not exactThe issue is that you integrated y with respect to x, and concluded that it was equal to y This is only viable if y = aex for some constant a, which we have no reason to suspect Solve y ^2x (\frac {dy} {dx})^2 = 1 using proposed change of variables Solve y2 −x(dxdy )2 = 1 using proposed change of variablesJiya22 is waiting for your help Add your answer and earn points



Using Euler Rsquo S Method Find An Approximate Value Of Corresponding To 1 Given That Dy Dx X 2 Y And Y 1 When X 0 Use The Step Size H 0 25




How To Solve Show The Differential Equations Are Exact 2xy Y Tany Dx X 2 X Tany 2 Secy 2 2 Dy 0 Te Tx 2x Dx Dt Xe Xt 0 Quora
Verify that x^2 cy^2 = 1 is an implicit solution to \frac {dy} {dx} = \frac {xy} {x^2 1} If you're assuming the solution is defined and differentiable for x=0, then one necessarily has y (0)=0 In this case, one can easily identify two trivial solutions, y=x and y=x If you're assuming the solution is defined andCalculus Basic Differentiation Rules Implicit Differentiation 1 AnswerSee it's pretty simple to solve, Since you are differentiating the equation with respect to x, that x² term when differentiated will become 2x Similarly that y² will become 2ymath\dfrac{dy}{dx}/math and that 5 being a con



Q Tbn And9gcq69xqaiwgxy95 44f5sqsm2pnlgxvor Roue6xadfczqpkv4qx Usqp Cau




Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When
So we get (1/y)(dy/dx) = log(2) 4) We want to find dy/dx, which is on the LHS To get this dy/dx on its own we can multiply both sides by y So we get dy/dx = y log(2) 5) To finish this question we need to sub in for y and then we have an answer for dy/dx Recall y=2^x (from our original question) So we get dy/dx = (2^x)(log(2)) => ourI think your question is (xy—1)/(xy—2)dy/dx=(xy1)/(xy2)(I) Solutionput (xy)=v then differentiate both sides with respect to 'x' we get 1dy/dx=dv/dxHere is the technique to find this derivative of the function and how to solve #Derivative#Calculus#Formula#Techniques




Engineering Mathematics Notes




Rd Sharma Class 12 Maths Solutions Chapter 11 Differentiation
Once y>x, then dy/dx=sqrt(2) * Y yields upward bound of y=exp(sqrt 2) * x, so no singularities Multiplying both sides by y, then substituting y*y=v yielded a similar interesting differential equation $\endgroup$ – Craig Stevens Aug 18 '18 at 1439Click here👆to get an answer to your question ️ If (x^2 y^2)^2 = xy , find dy/dxPatrick Musonda II originally asked this question Quora was unable to render the font he used in the browser, and I had to rewrite and answer it here



Solved Solve The Following Differential Equations X Y 3 Dx X Y 1 Dy 0 2 X Y 1 Dx 3x 4y 2 Dy C 3 1 Y 2 Xy 2 Dx X 2y Y 2xy Dy Course Hero




If X 1 Y Y 1 X 0 Then Prove That 1 X 2 Dydx 1 0
Calculus Find dy/dx y=1/ (x^2) y = 1 x2 y = 1 x 2 Differentiate both sides of the equation d dx (y) = d dx ( 1 x2) d d x ( y) = d d x ( 1 x 2) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more stepsThis is the Solution of Question From RD SHARMA book of CLASS 12 CHAPTER DIFFERENTIAL EQUATIONS This Question is also available in R S AGGARWAL book of CLASSTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Solve `(xy1)dx (2x 2y3)dy=0`




Implicit Differentiation Advanced Example Video Khan Academy



Solve Dy Dx Xy 1 X 2 X Y Sarthaks Econnect Largest Online Education Community
Given x 2/3 y 2/3 = a 2/3 y 2/3 = a 2/3 – x 2/3 Differentiate wrtx (2/3)y 1/3 dy/dx = 0 – (2/3)x 1/3 dy/dx = – (2/3)x 1/3 / (2/3)y 1/3 = x 1/3 /y 1/3 = (x/y) 1/3 Hence option (4) is the answer What is the solution to y/x (dy/dx) = sqrt (1 x^2 y^2 x^2 y^2)?12 x(y 1)dx ydy=0 iixydx (x^2 y^2) dy=0 ti(2x^3 xy^2 2y3)dx (x^2 y 2x)dy=0 Given the following differential equations ivy(x y 1)dx x(x 3y 2)dy=0 vy(6y^2 x 1)dx 2 xdy=0 v(x2y 4)dx (2xy= 5)dy=0 Vydx (3x– xy 2)dy=0 The differential equation(s) that can be solved by exact differential equations



Find Dy Dx When X And Y Are Connected By The Relation X2 Y2 2 Xy Studyrankersonline




Use Implicit Differentiation To Find Dy Dx Xy X Chegg Com
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more dy/dx=1x2y2x2y2, given that y=1 when x=0 Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to getFind dy/dx y^22x=xy y2 − 2x = xy y 2 2 x = x y Differentiate both sides of the equation d dx (y2 −2x) = d dx(xy) d d x ( y 2 2 x) = d d x ( x y) Differentiate the left side of the equation Tap for more steps By the Sum Rule, the derivative of y 2 − 2 x y 2 2 x with respect to x x is d d x y 2 d d x − 2 x d d x y




Misc 7 Show That General Solution Is X Y 1 A 1 X Y 2xy
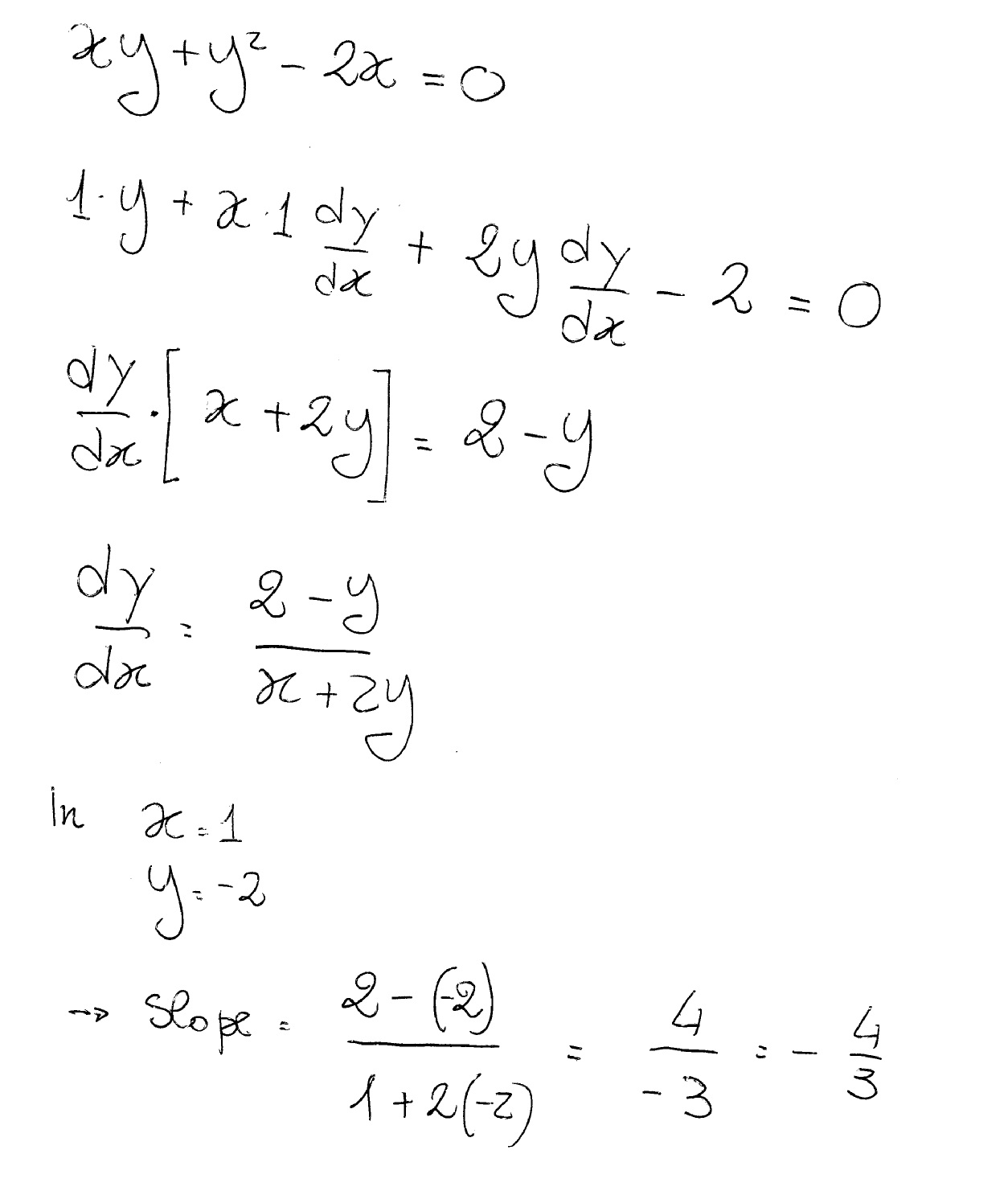



How Do You Differentiate Implicitly Xy Y 2x 0 To Find Dy Dx And Find The Slope Of The Curve At The Given Point 1 2 Socratic
KCET If 2x2y = 2xy, then (dy/dx) is (A) 2yx (B) 2yx 2xy (D) (2y1/2x1) Check Answer and Solution for above Mathematics question TardigradeIf x > 0, y > 0, z > 0, xy yz zx 1 and tan1 x tan1 y tan1 z = π, then x y z is equal to If X 1 Plus 2 Plus 4 By 2 8 By 3 Factorial 16 By 4 Fact Then X 1 Is Equal To If X 1 X 2 X 3 X N Are In Ap Whose Common Difference Is Alpha Then If X 13y 7 X Y Then Xy 1 Y If X 2x Plus 2 3x Plus 3 Are In Gp Then The Fourth Term IsSolve 1/(x y(x) 1)^2 ( dy(x))/( dx) (x^2/(x y(x) 1)^2 y(x)^2) = 0 Let P(x, y) = 1/(x y 1)^2 and Q(x, y) = y^2 x^2/(x y 1)^2 This is an exact



Www Tau Ac Il Levant Ode Solution 6 Pdf




Find Dy Dx If X2 Y2 2 Xy Brainly In
Why create a profile on Shaalaacom? If xyxy=1, find dy/dx Find the x− intercepts Find the y− intercept Find the equation of the line of symmetry Use all this information to sketch geometry Triangle PQR has vertices P(1,2), Q(25,2) and R(10,) Find the coordinates of the centroid Find the coordinates of the circumcenterThanks for the A!!




Using Runge Kutta Method Of Fourth Order Solve The Differential Equation M3 Notes Question Answer Collection
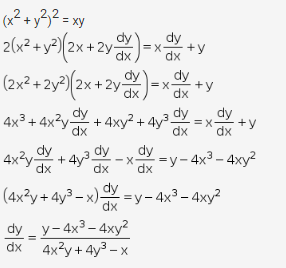



If X 2 Y 2 2 Xy Find Dy Dx Mention Each And Every Step Cbse Class 12 Learn Cbse Forum
Simple and best practice solution for (xy1)dx(2x2y1)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework Click here 👆 to get an answer to your question ️ Find dy/dx if x^1/2y^1/2=a^1/2 Jiya22 Jiya22 Math Secondary School answered Find dy/dx if x^1/2y^1/2=a^1/2 1 See answer Mark my ans as brainlist if u found it quite helpful Sure!! Find dy/dx (x) 1/2 (y) 1/2 = (a) 1/2 Mention each and every step If y = tan 1 a/x log (xa/xa) 1/2 , prove that dy/dx = 2a 3 /(x 4 – a 4 ) Mention each and every step Queries asked on Sunday & after 7pm from Monday to Saturday will be answered after 12pm the next working day



How To Find Dy Dx Of The Function Y X 1 X 2 X 1 2 Quora




Use Implicit Differentiation To Find Dy Dx In Chegg Com
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreSee the answer Show transcribed image text Expert Answer 100% (1 rating) Previous question NextThis is my differential equations practice #18 Give it a try first and check the final answer For differential equations problems requests, just c
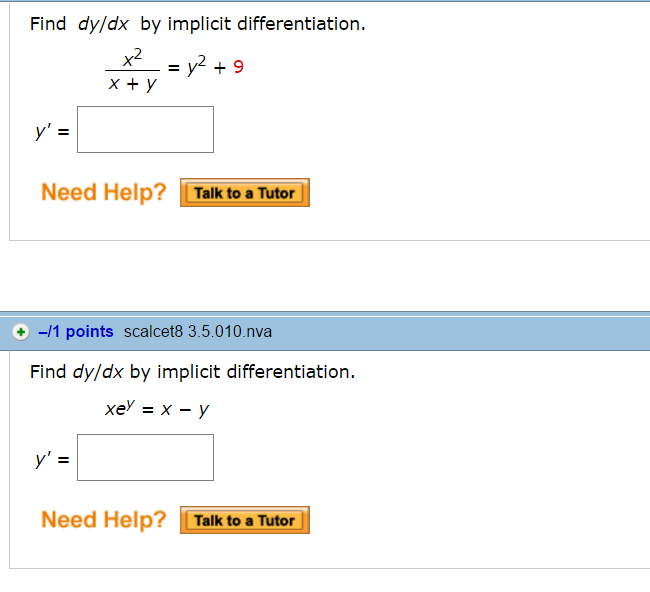



Find Dy Dx By Implicit Differentiation X 2 X Y Chegg Com




How Do You Find Dy Dx For Y 2x Sqrt X 1 Socratic
Click here👆to get an answer to your question ️ Find dy/dx of sin^2 x cos^2 y = 1 Join / Login > 12th > Maths > Continuity and Differentiability > Derivatives of Implicit Functions Solve y(x) 2 = (x y(x) 1) ( dy(x))/( dx) Rewrite the equation 2 y(x) (x y(x) 1) ( dy(x))/( dx) = 0 Let P(x, y) = y 2 and Q(x, y) = x y 1 This(b) 2 x y dx ( y 2 x 2) dy = 0 Here, M = 2 x y, M y = 2x, N = y 2 x 2, and N x = 2 xNow, ( N x M y) / M = ( 2 x 2 x ) / ( 2 x y) = 2 / yThus, μ = exp ( ∫ 2 dy / y ) = y2 is an integrating factor The transformed equation is ( 2 x / y ) dx ( 1 x 2 y2) dy = 0 Let m = 2 x / y, and n = 1 x 2 y2Then, m y = 2 x y2 = n x, and the new differential equation is exact




If Sqrt 1 X 2 Sqrt 1 Y 2 A X Y Show That Dy Dx Sqrt 1 Y 2 1 X 2 Mathematics And Statistics Shaalaa Com




If X 2 Xy Y 2 0 Then Find Dy Dx Brainly In
Find dy/dx given x^3 3 x^2 y 2 x y^2 = 12 Extended Keyboard; The nice thing about this differential equation is that the dy dx is already isolated, therefore the answer can be obtained by simply integrating both sides ∫dy = ∫3x 2 x2 dx y = 3 2x2 −2x−1 C y = 3 2x2 − 2 x C 2 = 3 2 (1)2 − 2 1 C 4 − 3 2 = C 5 2 = CY2x2 y2 d2y y dx2 dy O D X dx II Use logarithmic differentiation to find the derivative of y with respect to the independent variable y= (In x)Inx In (In x) 1 O A X In (In x) О в (In x)Inx X (Inx)Inx



X 2 Y 2 1 Find Dy Dx By Implicit Differentiation Youtube




If 2 X 2 Y 2 X Y Then Dy Dx Is Equal To 2 Y 2 X
Find dy/dx y3 – 3xy2 = x3 3x2y Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to Find the solution of the differential equation x√(1 y^2)dx y√(1 x^2)dy = 0 asked May 19 in Differential Equations by Yajna ( 299k points) differential equationsQuestion Solve The Initial Value Problems Dy/dx = X(y 2)/x^2 4 Y(1) = 5 Dy/dx = Y/x Y(2) = 3 Dy/dx = Y 1/x 1 Y(0) = 0 Dy/dx = Xy Y(1) = 2 Dy/dx = 2y 1 Y(0) = 1/2 Dy/dx = 1/2y 1 Y(0) = 1 Dy/dx = E^y Y = 0 When X = 1 Dy/dx = X/squareroot X^2 9 Y = 5 When X = 4 This problem has been solved!




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange
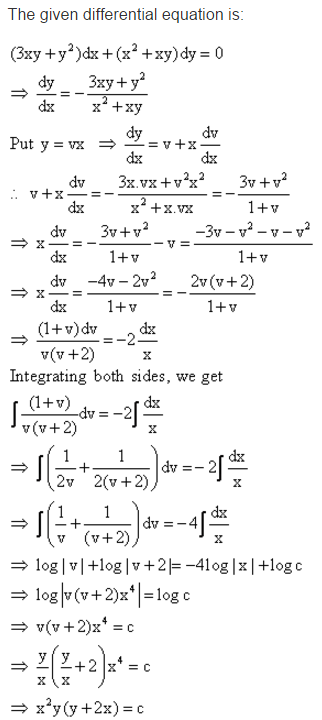



Find The Particular Solution Of Given Differential Equation 3xy Y 2 Dx X 2 Xy Dy 0 At X 1 Y 1 Mathematics Topperlearning Com D1ksg633
Free Multivariable Calculus calculator calculate multivariable limits, integrals, gradients and much more stepbystepCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music




Find Dy Dx If X 2 2xy Y 2 0 Brainly In








Find Dy Dx By Implicit Differentiation X 2 Y 2 Chegg Com



Solved Find The Particular Solution Indicated For The Following Course Hero



How To Find Dy Dx When Y Sin X 2 Y 2 Quora




Find Dy Dx When X 2 Y 2 4




X 2 Y 2 Xy Find Dy Dx Novocom Top




Show That The General Solution Of The Differential Equation Dy Dx Y 2 Y 1 X 2 X 1 0 Is Given By X Y 1 A 1 X Y 2xy Where A Is Parameter Mathematics Shaalaa Com




Solution Solve The Differential Equation X Y 1 Dx X 1 Dy 0 If



If X 2 Y 2 2 Xy Find Dy Dx Sarthaks Econnect Largest Online Education Community



Use Implicit Differentiation To Find Dy Dx And Then Chegg Com
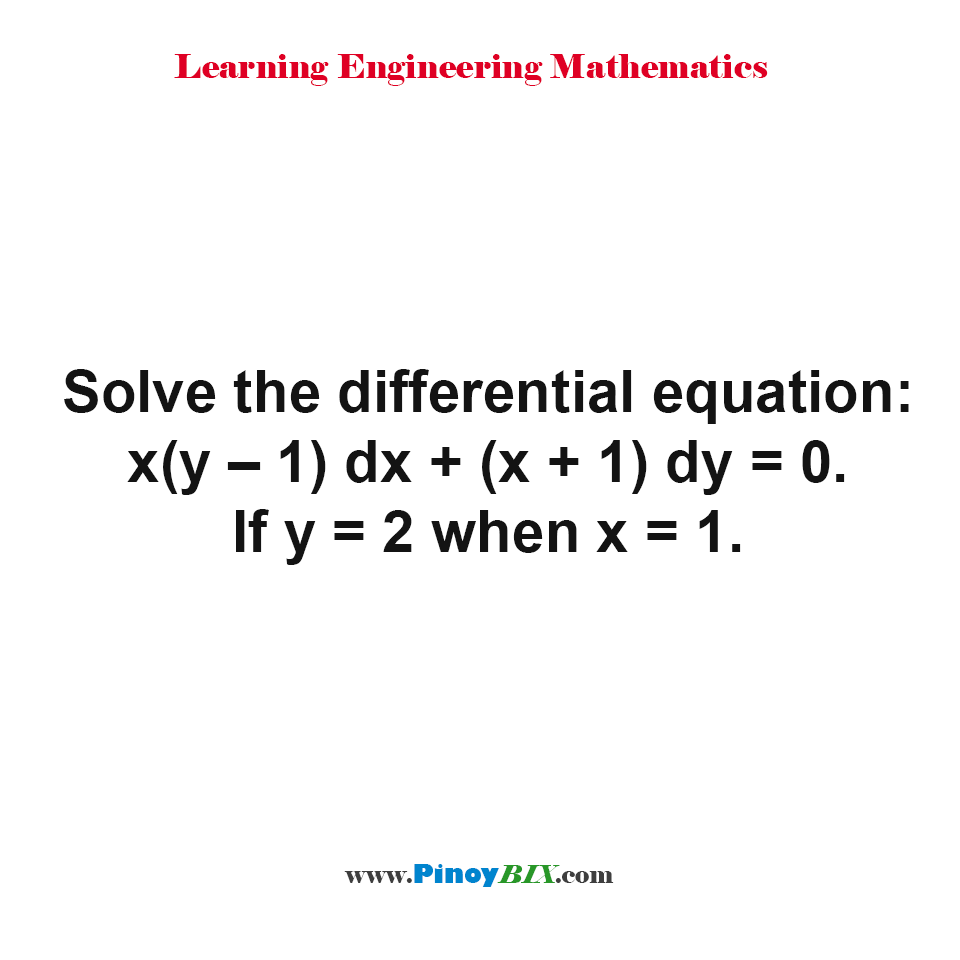



Solution Solve The Differential Equation X Y 1 Dx X 1 Dy 0 If Y 2 When X 1




Engineering Mathematics Notes




Answered Exexcises E Set 2 Implicit Differentia Bartleby




Ex 5 3 5 Find Dy Dx In X2 Xy Y2 100 Class 12




Find Dydx Where X 2 Y 2 3xy 1
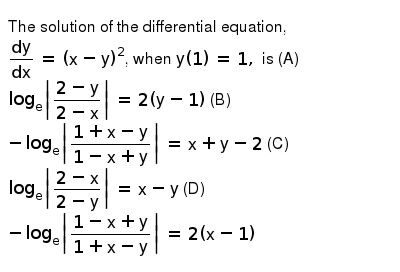



The Solution Of The Differential Equation Dy Dx X Y 2 Whe



Find Dy Dx When X And Y Are Connected By The Relation Sin Xy X Y X2 Y Studyrankersonline




Solve Y 1 Xy Dx X 1 Xy X 2y 2 Dy 0 Mathematics Stack Exchange




If U Sin 1 X 2 Y 2 X Y Then Show That X Du Dx Y Du Dy Tan U Mathematics 1 Question Answer Collection



Solve The Differential Equation Dy Dx 1 X Y2 Xy2 When Y 0 X 0 Studyrankersonline




X 2 Y 2 Xy Find Dy Dx Novocom Top




Implicit Differentiation




If Sin Xy X Y X 2 Y Find Dy Dx Brainly In




Slides Show



If Xy E X Y Then Prove That Dy Dx Log X 1 Log X 2 Sarthaks Econnect Largest Online Education Community




Engineering Mathematics Notes




Solve The Initial Value Problems X 2 Dy Dx 4x 2 Chegg Com



4 2 Implicit Differentiation



4 2 Implicit Differentiation



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q4 Pdf



3 8 Implicit Differentiation Calculus Volume 1
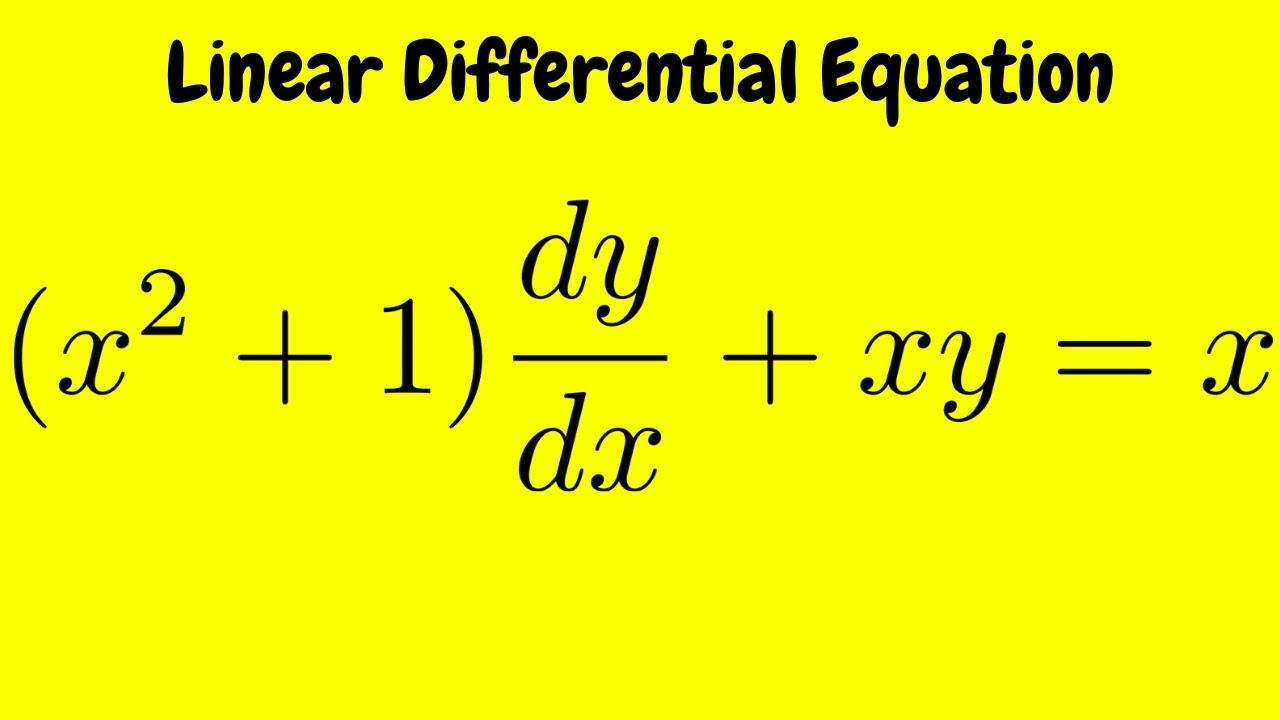



Solve The Linear Differential Equation X 2 1 Dy Dx Xy X Youtube




Section 3 1 1 Implicitly Differentiate To Find Dy Dx Y3 X2 4 Slideshow And Powerpoint Viewer 2 Implicitly Differentiate To Find Dy Dx Y 4 X 3 2x 4y 3 Dy 3x 2 2 Dx Dy 4y




Find Dx Dy For X2 Xy Y2 100 Mathematics Shaalaa Com




Implicit Differentiation



If 1 X 2 1 Y 2 A X Y Show That Dy Dx 1 Y 2 1 X 2 Sarthaks Econnect Largest Online Education Community




Find Dy Dx In The Following A X 3 X 2y X Y 2 Y 3 81




Math 432 Hw 2 5 Solutions
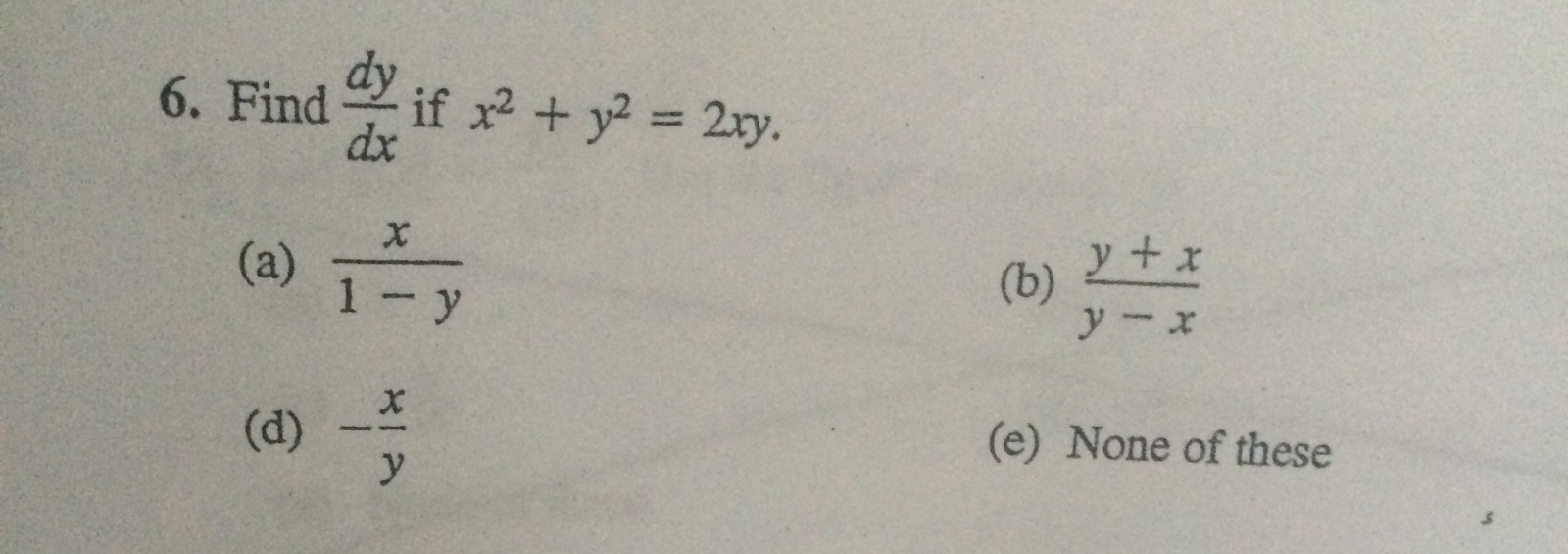



6 Find Dy Dx If X 2 Y 2 2xy A X 1 Y B Chegg Com




Find Dy Dx By Implicit Differentiation 2x 2 Xy Chegg Com




Engineering Mathematics Notes




Solve X Y 1 Dx 2x 2y 3 Dy 0 Youtube




If 2 X 2 Y 2 X Y Then Dydx Is Equal To




If X 2 Y 2 25 Then Find Dy Dx



1




Find Dy By Dx At X 1 Y Piby4 If Sin 2 Y Cos Xy K Mathematics Shaalaa Com




Ex 5 3 4 Find Dy Dx In Xy Y2 Tan X Y Chapter 5



Answered Rebecca Ferrer 2 26 Given Bartleby



1



1



Jntua Ac In Gate Online Classes Registration Downloads Material A Pdf




If X2 Y2 2 Xy Find Dy Dx Mention Each And Every Step Mathematics Topperlearning Com Gwvwfskk



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf



Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf




Ex 5 3 5 Find Dy Dx In X2 Xy Y2 100 Class 12




Q2 If X 2 Y 2 4 Find Dy Dx Implicit Function Differentiation If X2 Y2 4 Find Dy Dx Youtube




4 1 Implicit Differentiation



4 2 Implicit Differentiation




Solution Of Y Xy 1 Dx X 1 Xy X 2y 2 Dy 0 Mathematics Stack Exchange



Find Dy Dx Of X 2 Y 2 2 4xy Sarthaks Econnect Largest Online Education Community




X 2 Y 2 Xy Find Dy Dx Novocom Top




If Y X X2 1 1 2 M Then Show That X2 1 D2y Dx2 X Dy Dx M2y 0 Mathematics Topperlearning Com 6jd9kell




Worked Example Implicit Differentiation Video Khan Academy




4 1 Implicit Differentiation



How To Solve 1 X 3 Dy Dx X 2 Y Quora
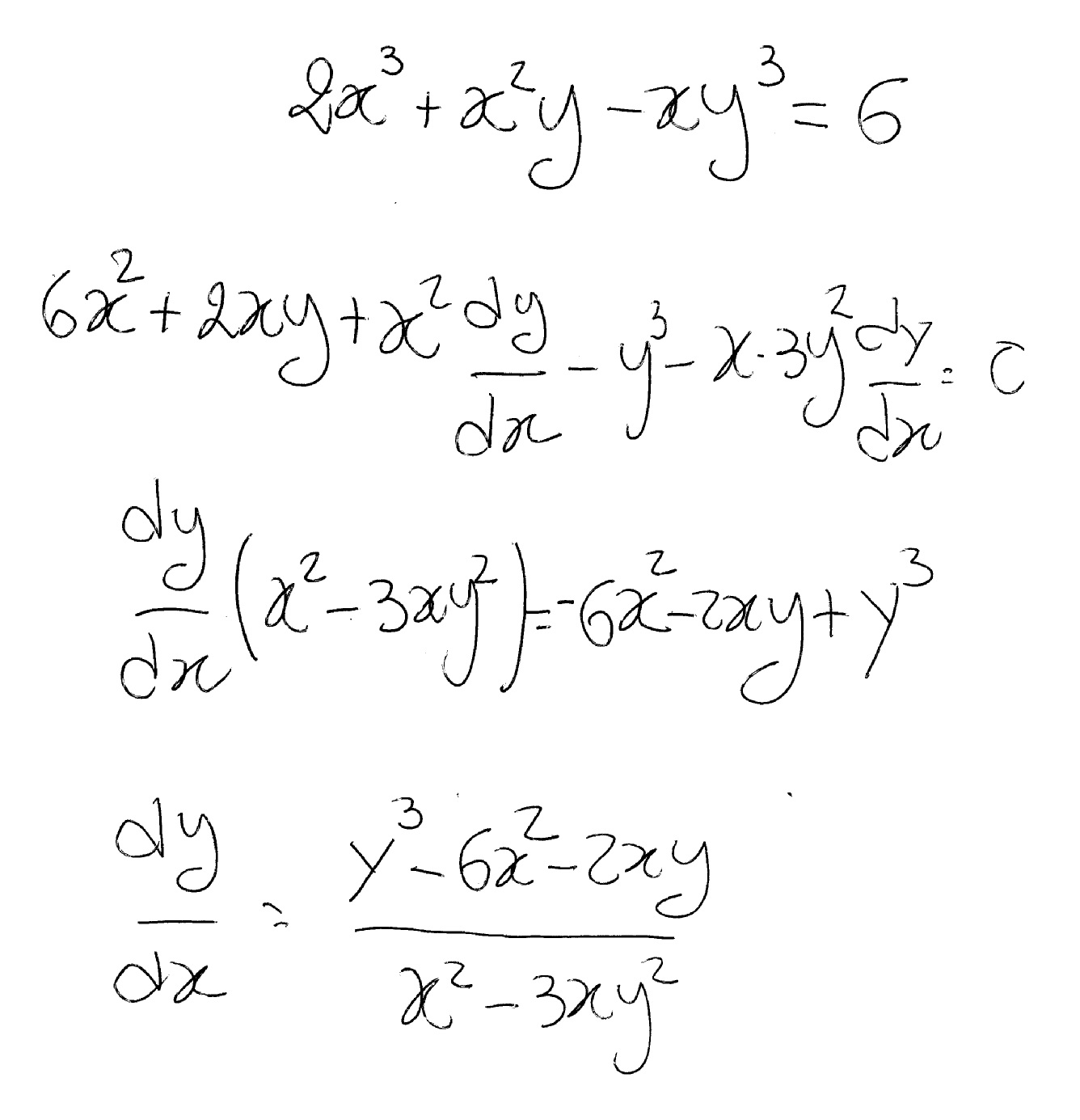



How Do You Find Dy Dx By Implicit Differentiation For 2x 3 X 2 Y Xy 3 6 Socratic




Ex 9 4 16 For Xy Dy Dx X 2 Y 2 Find Solution



Www Math Colostate Edu Clayton Teaching M113f10 Homework Hw7solutions Pdf



Using Euler Rsquo S Method Find An Approximate Value Of Corresponding To 1 Given That Dy Dx X 2 Y And Y 1 When X 0 Use The Step Size H 0 25




Implicit Differentiation



Using Euler Rsquo S Method Find An Approximate Value Of Corresponding To 1 Given That Dy Dx X 2 Y And Y 1 When X 0 Use The Step Size H 0 25



Solve 2 Y 3 Xy Dy Dx 0 Given That Y 1 2 Studyrankersonline



How To Find Dy Dx Of This Problem X Siny Xy Quora




15 The Differential Equation 2xy Dy X2 Y2 1 Dx Determines A A Family Of Circles With Centre On X Axis B A Family Of Circles With Centre On Y Axis




Find The Particular Solution Of The Following Differential Equa



0 件のコメント:
コメントを投稿